Wir schauen uns das Boxplot anhand konkreter Daten an, die dir als Colab Notebook zur Verfügung stehen. Ganz konkret: Eine Gruppe von Wissenschaftlern forscht in Bezug auf die Körpergröße von Menschen unterschiedlicher Ortschaften. Zu diesem Zweck haben sie die Körpergröße einiger Menschen in den Städten “Dorftown”, “Stadtort” und “Megacity” gemessen und zusammengetragen.

# Stichproben
    'Dorftown': [160, 165, 163, 169, 170, 172,
                 172, 175, 185, 220],
    'Stadtort': [150, 155, 152, 153, 154, 162,
                 165, 170, 180, 185],
    'Megacity': [140, 150, 160, 170, 180, 190,
                 200, 210, 240, 250]

Die Daten verdeutlichen, dass wir drei Stichproben mit je zehn Messungen haben, also insgesamt 30 Datenpunkte.

Wie du sehen wirst, eignet sich für die Visualisierung ein Boxplot ideal, denn es ist ein einfaches, aber leistungsstarkes Werkzeug zur nachvollziehbaren Darstellung einer Datenverteilung. Besonders nützlich ist es, wenn du schnell Gruppen miteinander vergleichen möchtest (in unserem Beispiel also die Städte), weil es die folgenden statistischen Kennzahlen eines Datensatzes grafisch zusammenfasst:

• Zentrale Tendenz: Mittelwert, Median und Modus (auch Modalwert genannt)
• Streuung
• Potenzielle Ausreißer

Abschnitte:
1. Was ist ein Boxplot
2. Interpretation unseres Boxplots als Beispiel
3. Wann macht ein Boxplot Sinn?
5. Vor- und Nachteile
6. Fazit

Was ist ein Boxplot

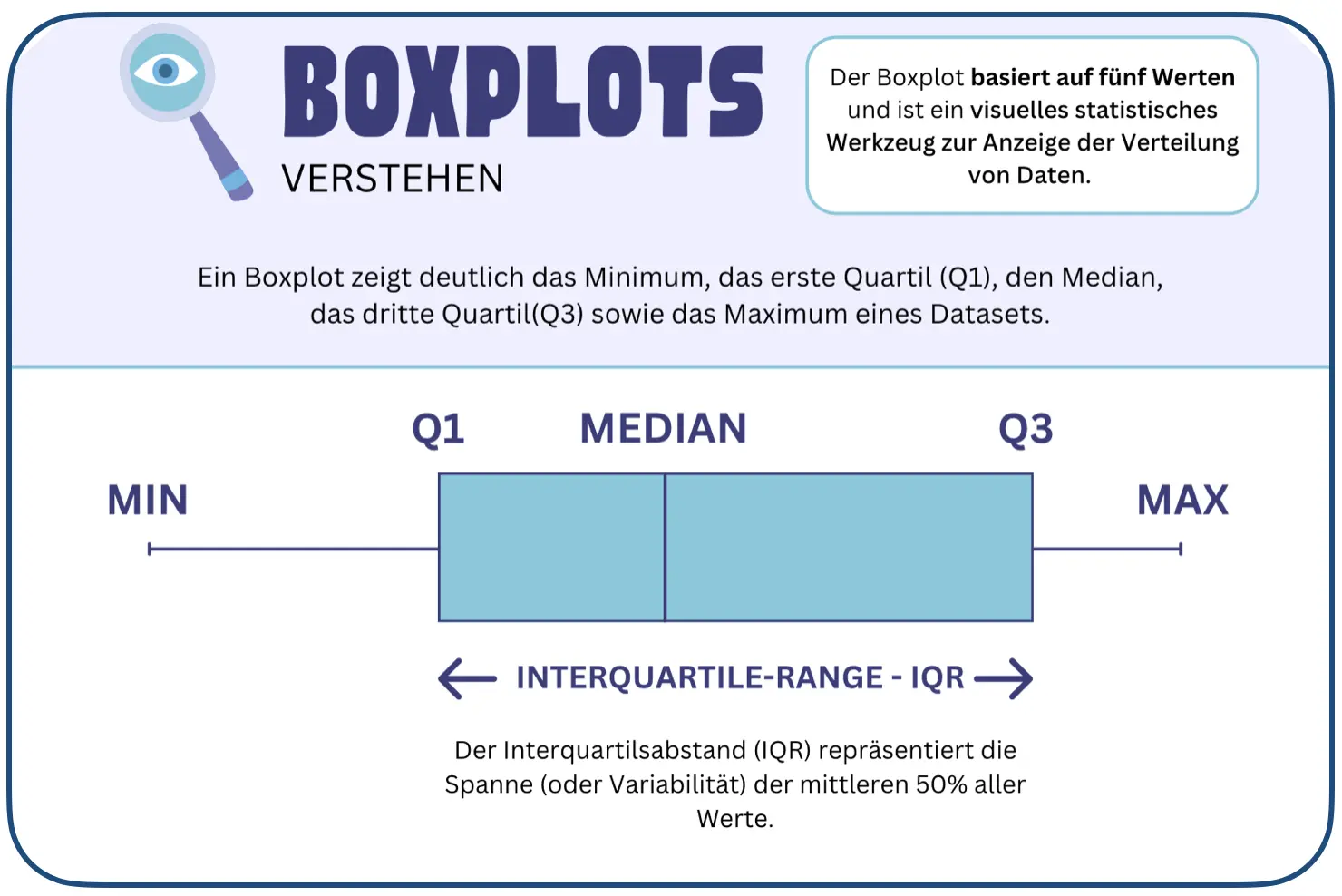
Das Boxplot nennt man auch “Box-and-Whisker-Plot”. Es ist ein Diagramm, welches die Verteilung numerischer Daten darstellt, wobei es auf fünf wesentlichen deskriptiven Statistiken basiert. Wenn die die folgenden Kennzahlen nichts sagen, lies kurz den Beitrag ”Quartil” - dort sind sie erklärt:

• Minimum: Der kleinste Datenpunkt (ohne Ausreißer).
• Erstes Quartil (Q1): Der Median der unteren Hälfte des Datensatzes (25. Perzentil).
• Median (Q2): Der mittlere Wert des gesamten Datensatzes (50. Perzentil).
• Drittes Quartil (Q3): Der Median der oberen Hälfte des Datensatzes (75. Perzentil).
• Maximum: Der größte Datenpunkt (ohne Ausreißer).

Ein Boxplot besteht typischerweise aus einer Box, die den Interquartilsabstand (IQR) zwischen Q1 und Q3 darstellt, und zwei „Whiskers“, die sich bis zu den minimalen und maximalen Datenpunkten erstrecken. Ausreißer, falls vorhanden, tauchen als einzelne Punkte außerhalb der Whiskers auf, wie hier in hellblau zu sehen ist.

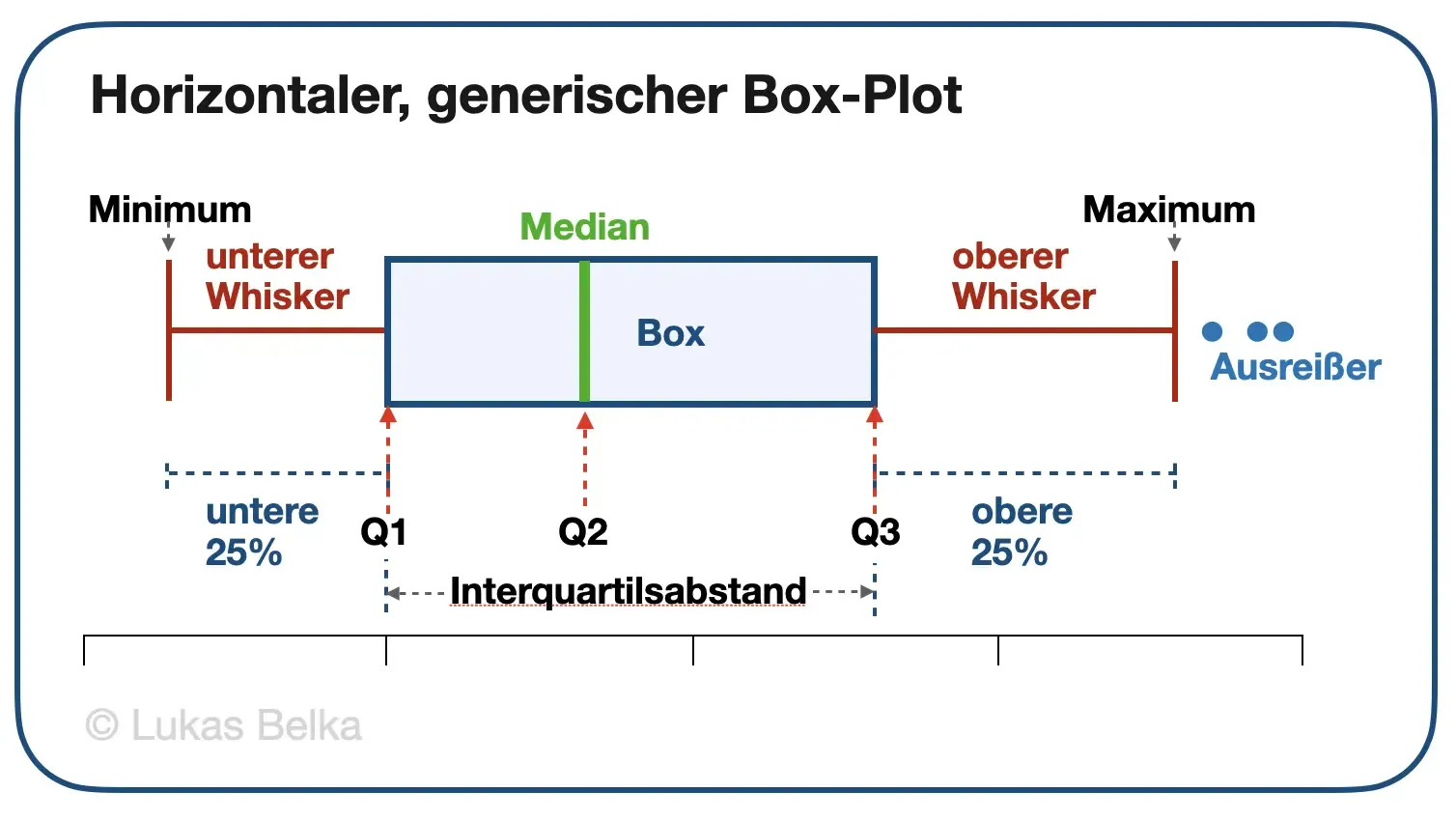
Wichtige Elemente sind:

• Die Box: Der rechteckige Teil des Plots erstreckt sich vom ersten Quartil (Q1) bis zum dritten Quartil (Q3) und zeigt den Interquartilsabstand (IQR). Der IQR enthält die mittleren 50 % der Daten.

• Die Medianlinie: Eine Linie innerhalb der Box stellt den Median (Q2) dar, der den zentralen Wert des Datensatzes anzeigt.

• Die Whisker: Linien, die sich von der Box aus erstrecken, zeigen den Bereich der Daten ohne Ausreißer. Diese Whiskers erstrecken sich typischerweise bis 1,5 mal den IQR über Q1 und Q3 hinaus, obwohl dies je nach verwendeter Software variieren kann.

• Ausreißer: Punkte, die außerhalb der Whiskers liegen, gelten als Ausreißer. Diese werden oft als einzelne Punkte oder Kreise markiert, um zu signalisieren, dass sie ungewöhnlich weit von den übrigen Daten entfernt sind.

Interpretation unseres Boxplots als Beispiel

Boxplots sind besonders nützlich, um Verteilungen zwischen Gruppen zu vergleichen, Schiefe (Links- oder Rechtsschief) zu erkennen und Ausreißer zu identifizieren. Lass uns die wichtigsten Komponenten anhand unserer Daten interpretieren.

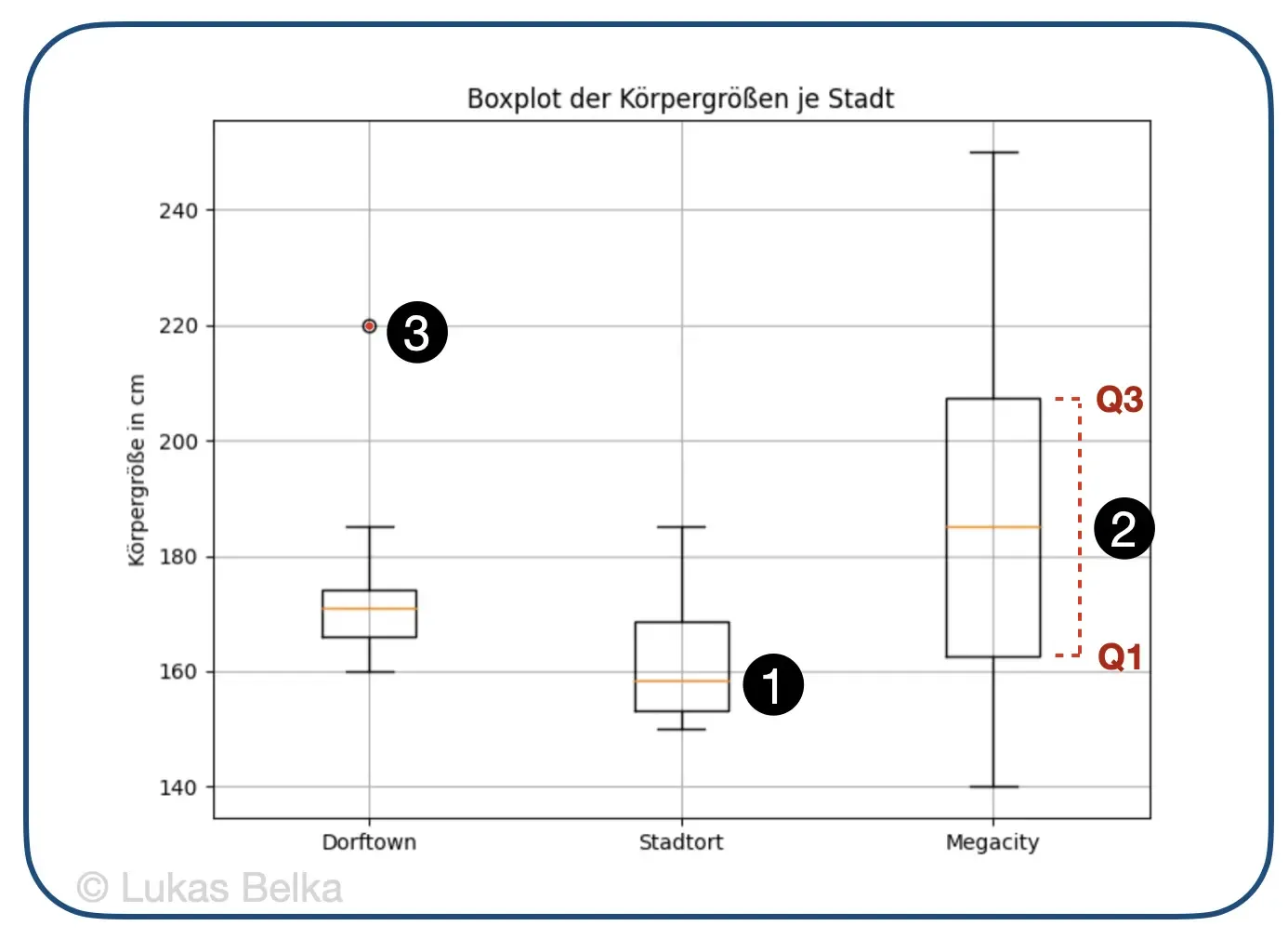
1. Verteilungsform: Wenn der Median (orangener Strich) in der Mitte der Box liegt, ist die Verteilung der Daten symmetrisch. Wenn der Median näher an Q1 oder Q3 liegt, sind die Daten schief verteilt (linksschief, wenn näher an Q3, rechtsschief, wenn näher an Q1). Für “Stadtort” zeigt das mittlere Boxplot, dass die Daten leicht linksschief sind, da der Median (orange) näher am ersten Quartil liegt.

2. Streuung der Daten: Die Größe der Box (IQR) zeigt die Streuung der mittleren 50 % der Daten. Eine größere Box weist auf eine größere Variabilität der Daten hin. Längere Whiskers deuten auf eine breitere Gesamtspanne hin, während kürzere Whiskers auf weniger Variabilität hindeuten. Am Beispiel von “Megacity” können wir sehen, dass die gemessenen Körpergrößen insgesamt breiter gesteut sind und auch die Box (die mittleren 50% von Megacity’s Daten) eine höhere Varianz aufweisen.

3. Ausreißer: Punkte, die außerhalb der Whiskers erscheinen, gelten als Ausreißer. Diese könnten eine weitere Untersuchung rechtfertigen, um zu verstehen, warum sie von den meisten Daten abweichen. In “Dorftown” lebt eine Person mit 220cm Körpergröße, was angesichts der übrigen Messwerte außergewöhnlich erscheint. Da die Whisker im Normalfall bis zu 1,5 mal so groß sind, wie der Interquartilsabstand (IQR), taucht dieser Punkt als Ausreißer auf.

Gesamtbild: Man würde in einer ausführlichen Datenanalyse zudem noch die Boxen miteinander Vergleichen und auf die Unterschiede innerhalb der Gesamtheit aller Daten eingehen. Da es hier lediglich um die Boxplots geht, belassen wir es bei den drei genannten Punkten.

Wann macht ein Boxplot Sinn?

Wie du anhand unseres Beispiels siehst, verwendest du einen Boxplot, wenn du:

• Verteilungen zwischen verschiedenen Gruppen vergleichen möchtest (z. B. Vergleich von Testergebnissen zwischen verschiedenen Klassen oder Einkommensniveaus zwischen Regionen).
• Ausreißer in einem Datensatz identifizieren möchtest, die die Analyse beeinflussen könnten.
• Große Datensätze zusammenfassen möchtest, indem Sie eine visuelle Darstellung bietest, welche die wesentlichen Merkmale der Verteilung einfängt, ohne jeden Datenpunkt zu zeigen.

Boxplots verwendet man häufig in der explorativen Datenanalyse (EDA), um schnelle Einblicke in die Daten zu gewinnen, bevor man komplexere statistische Methoden anwendet.

Vor- und Nachteile

Vorteile
Einfachheit: Boxplots sind leicht zu interpretieren und zu erstellen.
Vergleichbarkeit: Sie ermöglichen den schnellen Vergleich mehrerer Datensätze.
Ausreißererkennung: Boxplots machen es einfach, Ausreißer zu erkennen, die die Ergebnisse Ihrer Analyse beeinflussen könnten.

Nachteile
Begrenzte Details: Im Gegensatz zu Histogrammen oder Dichteplots zeigen Boxplots nicht die genaue Verteilung der Datenpunkte (z. B. die Anzahl der Modi oder Cluster).
Für kleine Datensätze bedingt geeignet: Bei sehr kleinen Datensätzen zeigt der Boxplot möglicherweise keine Muster oder Variabilität effektiv.

Fazit

Ein Boxplot ist ein unverzichtbares Werkzeug im Toolkit jedes Data Analysts und bietet eine simple Möglichkeit, die Verteilung prägnant zu visualisieren und sowohl die zentrale Tendenz, als auch die Streuung von Daten zu zeigen. Er ist besonders nützlich beim Vergleich von Gruppen und bei der Identifizierung von Ausreißern. Das hilft bessere Entscheidungen auf Basis der Daten zu treffen.