Definition

Quartile tauchen häufig in Verbindung mit Boxplots auf und sind spezielle Werte, die einen geordneten Datensatz in vier gleiche Teile unterteilen. Sie helfen dabei, die Verteilung der Daten besser zu verstehen, indem sie bestimmte Bereiche in den Daten angeben. Die Quartile sind:

1. Erstes Quartil (Q1): Markiert das untere Viertel des Datensatzes und trennt diese unteren 25 % der Daten von den oberen 75 %.
2. Zweites Quartil (Q2): Dies ist der Median und trennt die Daten in zwei Hälften (50 %).
3. Drittes Quartil (Q3): Ist das obere Viertel des Datensatzes und trennt die unteren 75 % der Daten von diesen oberen 25 %.

Du findest weiter unten die Veranschaulichung mittels Boxplot

Bevor du in das folgende Beispiel einsteigst, solltest du wissen, wie der Median bestimmt wird. In der kurzen Erläuterung des Median erfährst du, worauf es bei der Bestimmung im Hinblick auf ungerade oder geraden Zahlenreihen ankommt.

Beispiel

Nehmen wir an unser Datensatz beinhaltet die folgenden Zahlen, die ihrer Größe nach von klein nach groß sortiert sind:

3, 7, 8, 12, 15, 18, 21, 24, 27, 30

• Zunächst bestimmen wir den Median - das zweite Quartil (Q2): Der Median ist der Wert in der Mitte des Datensatzes. Da wir 10 Zahlen haben und somit eine gerade Zahlenreihe vorliegt, nehmen wir den fünften und sechsten Wert und dividieren das Ergebnis durch zwei.

  Q2 = 16,5, denn:

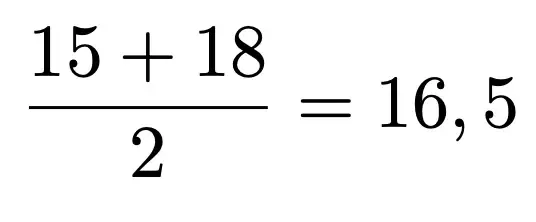
• Als nächstes bestimmen wir das erste Quartil (Q1): Q1 ist der Median der unteren Hälfte der Daten, also der ersten 5 Zahlen: 3, 7, 8, 12, 15. Bei dieser ungeraden Zahlenreihe lesen wir den mittleren Wert ab - dies ist die 8.

  Q1 = 8

• Zu guter letzt bestimmen wir das dritte Quartil (Q3): Q3 ist der Median der oberen Hälfte der Daten und somit der letzten 5 Zahlen: 18, 21, 24, 27, 30. Diesen können wir ebenfalls in der Mitte ablesen - es ist die 24.

  Q3 = 24

Zusammengefasst sind die Quartile:

• Q1 = 8
• Q2 = 16,5 (Median)
• Q3 = 24

Fazit

Die Quartile helfen uns, den Datensatz in gleich große Abschnitte zu unterteilen und zu verstehen, wie die Werte bzw. Daten im Datensatz verteilt sind. Dabei berücksichtigen sie möglich Ausreißer.

Der Interquartilsabstand (IQR - Interquartile-range)

Als Interquartilsabstand (engl.: Interquartile-range - IQR) wird die Differenz zwischen dem dritten und ersten Quartil bezeichnet. Er gibt die Spannweite der Mittleren 50% der Daten an.

Formel:
IQR = Q3 - Q1

Für unseren Datensatz (3, 7, 8, 12, 15, 18, 21, 24, 27, 30) beträgt der Interquartilsabstand 16, denn:

24(Q3) - 8(Q1) = 16.

IQR = 16

Veranschaulichung mittels Boxplot

Unser Datensatz ergibt den folgenden Boxplot - die relevanten Punkte sind eingezeichnet.

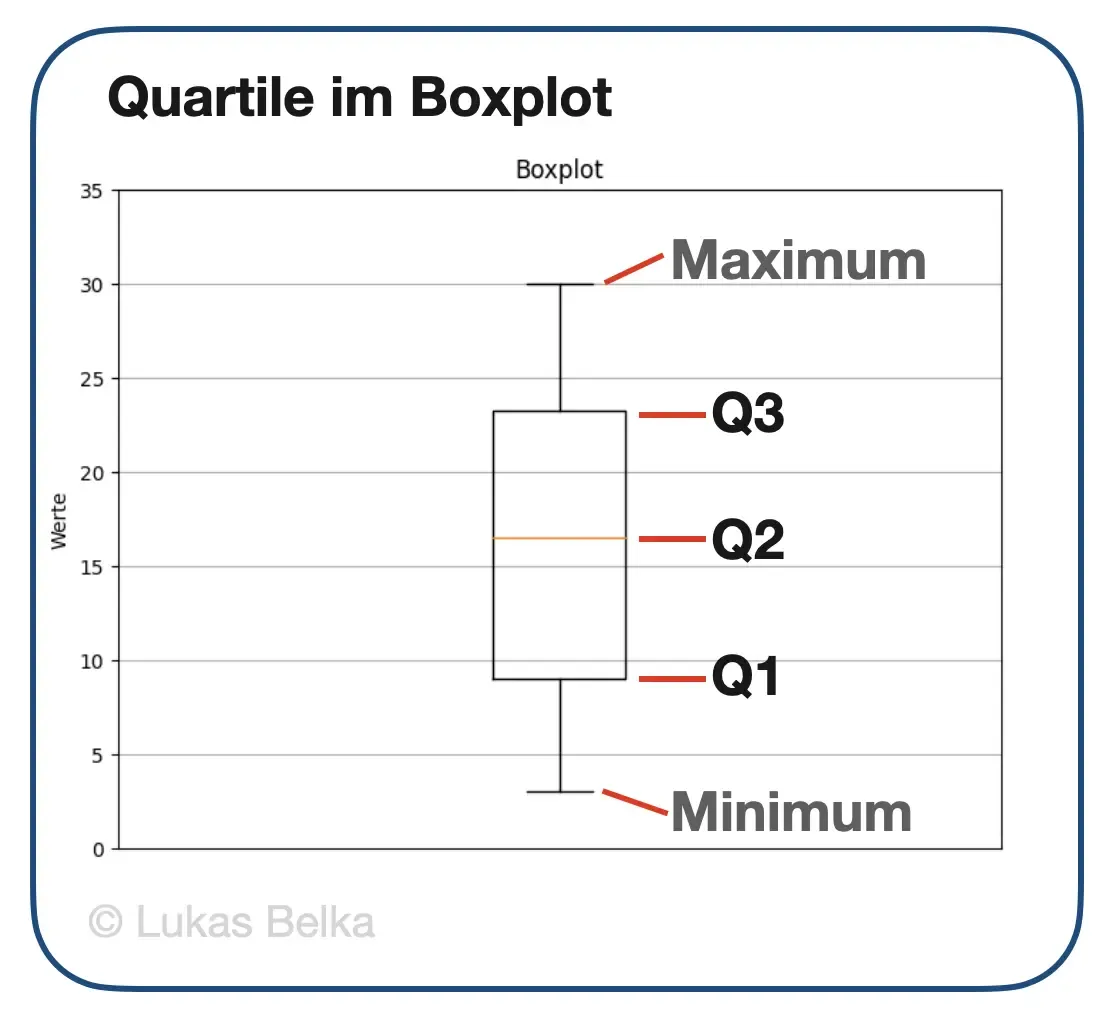
Hinweis: Hier findest du übrigens den Code für das Boxplot als Colab Notebook.